To assist educators and students with school projects about the Golden Gate Bridge, a number of resources are available through this website that can be used for research. We encourage you to start your learning experience by reading the entire History & Research section of our website.
Make a Model of the Golden Gate Bridge
To make a model of the Golden Gate Bridge, we offer the following:
There are a variety of Golden Gate Bridge model kits available online as well.
Common Math Questions
Hyperbola
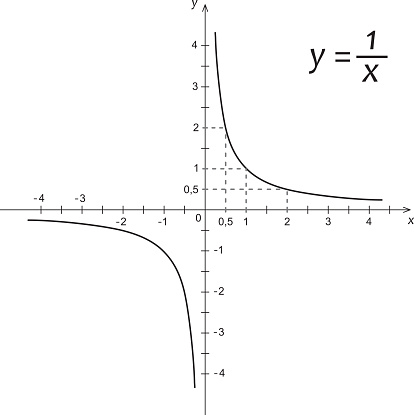
The main span of the Bridge (section between main towers) is effectively part of a hyperbola or the "top" part of a hyperbola. To make a graph of it, use three points on the curve as follows:
- North Tower, Point 1: (0, 746)
- Middle of the Bridge, Point 2: (2100, 246)
- South Tower, Point 3: (4200, 746)
Parabola
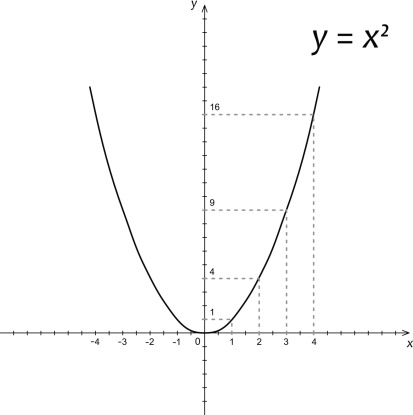
Each side (north and south) of the main towers (they are called side spans) is a parabola. The total distance on the x-axis of each parabola is 1,125 feet and the change in height on the y-axis is 500 feet. One can be shown as an increasing exponential and the other as a decreasing exponential.
If you wanted to represent the Bridge as one single curve, it would be a "4th order" curve, or something similar to this:
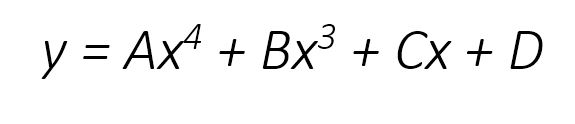
Using Math for Arches, Geometry and Load
There are two kinds of arches in bridge: Tension and compression.
- Tension arches are typically seen in suspension bridges like the Golden Gate Bridge where two main cables form the arch shape. The vertical deck load carried by the structure is transferred to a tensile force in the cable.
- Compression arches are typically seen in truss bridges where steel or concrete form the arch shape. Similarly, the vertical deck load carried by the structure is transferred to a compressive force in the steel or concrete.
The general mathematical formula that determines the shape of both the tension and compression arches is parabolic, meaning the formula has the typical form:
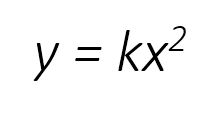
The inherent property of arches and how they support vertical load determines the parabolic formula in calculating their shape. For a given arch, the formulas relating the geometry and the resultant loads in the members are as follows:
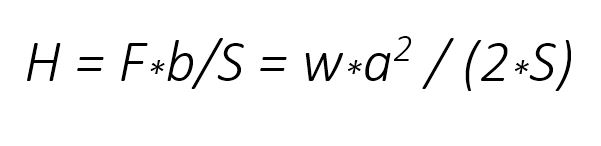
where;
- "H" is the horizontal component of tension in the arch.
- "F" is the total weight supported by the deck section between the lowest point and the highest point or "w*a".
- "b" is half the horizontal distance from the lowest point of the arch to the highest point (or 1/4 of the total span).
- "S" is the vertical distance from the lowest point to the highest point.
- "w" is the unit load supported by the arch.
- "a" is the horizontal distance from the lowest point of the arch to the highest point or half the span typically for a suspension or arch bridge.
To determine the arch shape for a particular bridge, engineers and architects can use the formula above and adjust the parameters of "S" and "H" to determine the optimum shape of arch for the span the bridge is intended to serve. For example, if the bridge is to span 100 feet and the unit weight on the deck is 10 lbs/ft and the cable can only support 500 lbs maximum horizontal force, the arch height "S" is determined as follows:
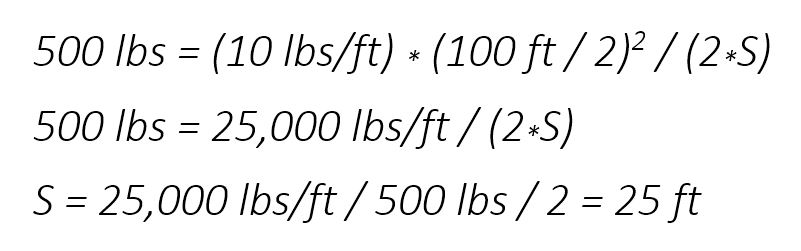
Therefore, the arch will be 100 feet in length and 25 feet high with a parabolic shape. If this shape does not serve the purposes of the engineer or architect (for example, if it is too tall and interferes with the views of neighbors, or if the tower supporting the cable is in the flight path of incoming airplanes), the engineer can use a stronger cable so that the height may be reduced. The other parameters such as the span and unit weight are typically fixed by the constraints of the site and the weight of the vehicles the bridge is intended to support. Try using a 1000 lbs horizontal capacity cable and see what the height of the arch is now. (The answer is 12.5 ft.)